Lecture 11 - Integer Arithmetic, Karatsuba Multiplication

This lecture focuses on performing arithmetic operations on large integers. We first cover Newton’s method for approximation, followed by Karatsuba multiplication.

Newton’s Method

Newton’s method is a method for finding the root of a function through successive approximation . It is based on the idea of linear approximation. Given a function $ f(x) $, we can approximate it’s root using the following steps -

• Start with an initial guess $ x_i $
• Compute the tangent line at $ x_i $
• Find the x-intercept of the tangent line
• Repeat the process with the new x-intercept

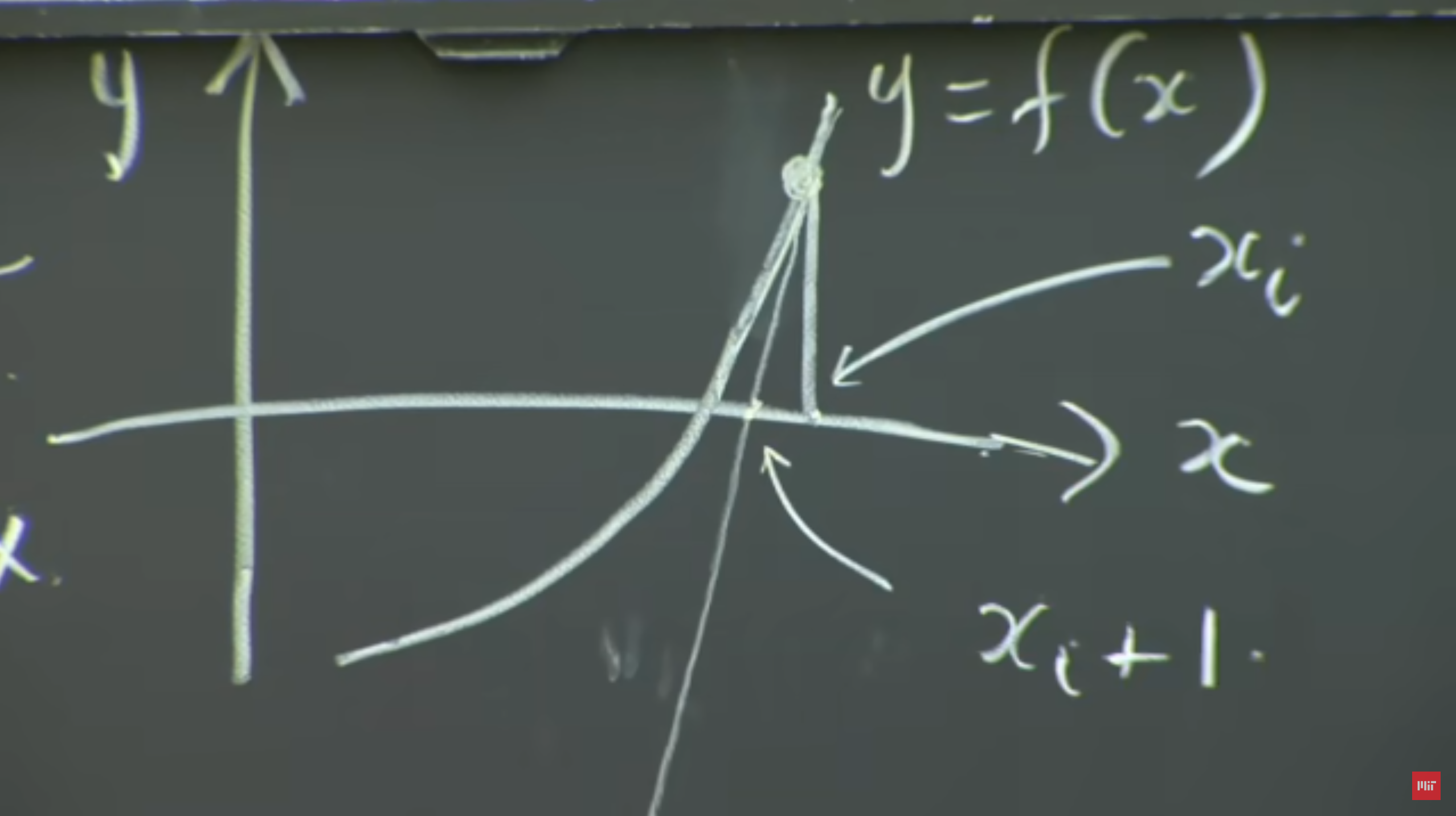
The formula for Newton’s method is given by -

$ x_{i+1} = x_i - \frac{f(x_i)}{f’(x_i)} $

$ x_{i+1} $ is an approximation of the root of the function $ f(x) $, which gets better on every iteration. Newton’s method converges quadratically, which means that the number of correct digits doubles on every iteration. This means that to get an approximation with $ n $ correct digits, we need to perform $ O(log\,n) $ iterations.

Karatsuba Multiplication

Karatsuba multiplication is a fast multiplication algorithm that uses divide and conquer to multiply two numbers. It is defined as follows -

• Given two numbers $ x $ and $ y $, we can write them as -
  • $ x = 10^{n/2}a + b $
  • $ y = 10^{n/2}c + d $
• The product of $ x $ and $ y $ can be written as -
  • $ xy = 10^nac + 10^{n/2}(ad + bc) + bd $
• We can recursively compute the product of $ a $ and $ c $, $ b $ and $ d $, and $ (a+b) $ and $ (c+d) $ to get the final product.