Regular Expressions, Context-Free Grammars
Regular Expressions to DFAs
Regular expressions are basically equivalent to DFAs. To show this, we have to show that, given a regular expression, we can design a DFA that accepts the same language as the regular expression, and given a DFA, we can write a regular expression that accepts the same language as the DFA.
To prove the first part of the implication, regular expression $\to$ DFA, we first show that we can design an NFA to represent a regular expression. We then know how to convert from an NFA to a DFA.
Regular expressions have three important operations - union, concatenation, and the * operation (zero or more). Suppose we have a regular expression without any of these operations, then this regular expression can be represented by a simple NFA that looks like a simple path. If the regular expression is 0110, for example, the NFA would just be a start node, followed by 4 other nodes, which it reaches if it reads the characters 0110 in sequence, the last of which is the accepting state.
So we can easily design an NFA for a regular expression that doesn’t use any operations. Now we show that if any two regular expressions are combined with an operation, then we can combine the corresponding NFAs for the two expressions using a simple method. The methods are shown in the photo below -
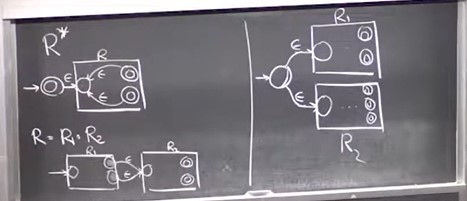
If the expressions are combined using the union operation - 01|10, then we just take the two NFAs for the two expressions and put a common start state before both of them with null transitions to the start states of the two NFAs. Think of this as similar to an OR gate.
If the expressions are concatenated, think of this as similar to an AND gate.
If an expression has the * operation, we add transitions from the accepting state back to the start state with null transitions, as shown above.
DFAs to Regular Expressions
To convert from a DFA to a regular expression, we first convert from a DFA to a GNFA. A GNFA stands for General NFA. A general NFA is just like an NFA, but its transitions function operates on regular expressions instead of an alphabet. So you can have regular expressions on the arrows between states.
For our purposes, we will make GNFAs satisfy the constraint that they only have one start state with only outgoing edges, and only one accepting state with only incoming edges. Once we convert from a DFA to a GNFA with some number of states k, we reduce the k states down to 2 (as shown in the lecture, pretty straightforward). Once we are left with 2 states in our GNFA, we can write it as a regular expression.
Context-Free Grammars
A context-free grammar is a set of rules for generating any string in a language. It can be defined by the following tuple - (V, $\Sigma$, R, S). V is the set of variables for the grammar, $\Sigma$ is the alphabet of the language we are going to generate, R is the set of rules for generating the language, and S is the start variable from which we start generation.
An example of a context-free grammar is

Languages that are generated from a context-free grammar are called context-free languages. As you might expect, since CFG is a more powerful model of computation as compared to regular expressions or DFAs, regular languages are a subset of context-free languages. That is, every regular language is a context-free language (i.e. can be expressed with a CFG).
Pushdown Automata
Pushdown automata (PDAs) are a more powerful variation of NFAs. Think of them as basically NFAs with access to a stack onto which they can push items and pop items. They allow us to express a larger set of languages.
Even though NFAs are equivalent to DFAs, PDAs are not equivalent to their deterministic counterparts. That is, DPDAs $\ne$ PDAs.