Lecture 3 - Finite State Automata & Regular Languages

Finite Automata

A finite automaton is the same as a finite state machine. It has a finite set of states that it can be in, and it takes input from a set called its alphabet. It has a transition function that takes one alphabet and the current state as input and transitions to the next state.

The notation we will use for these quantities is the following -

$ Q $	Finite set of states
$ \Sigma $	Finite alphabet
$ \delta: Q \times \Sigma \rightarrow Q $	Transition function
$ q_0 $	Start state
$ F \subset Q $	Accepted states

We call \(L = 0^{*}\) a language. In this case, a language is the set of all binary strings of length 0 or more. A language is just any set of strings. We say that a language is accepted or recognized by an automaton if the automaton ends up in an accepting state for all strings in the language, and we denote that as $ L(M) $, meaning $L$ is a language recognized by the finite automaton $M$. We say that $L$ is a regular language if we can design an automaton to accept that language.

Regular languages have the following properties -

1. The intersection of regular languages is regular
2. Complement of a regular language is regular
3. Regular languages are closed under union, intersection and complement
4. All finite languages are regular

An example of a language that is not regular is the language of all palindromes. We can prove this using the pigeonhole principle. A finite state automaton has a finite number of states, and this language can have strings of infinite length. Since the amount of “memory” a finite automaton has is essentially equal to the number of states it has, it cannot store inputs whose length is more than the number of states it has. Therefore, we cannot design a finite state automaton for this language, so it is not regular. This was just a rough proof, but the lecture gives a detailed proof.

Nondeterministic Finite State Automata

A non-deterministic finite state automaton is an extension of DFAs. It has the property that it can have any number of ways to transition from one state to another, even when it reads the same symbol. That means that if it is in a state $q_i$, it can have any number of paths to follow when it reads the symbol 0, for example, whereas a DFA only has one path per symbol.

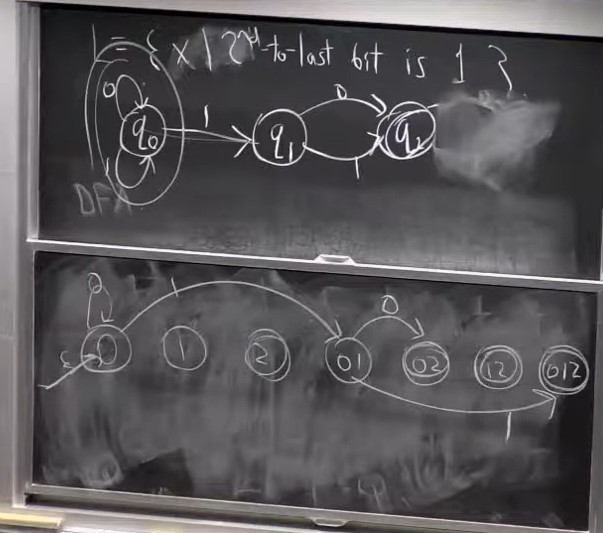
For example, we have the NDFA that accepts the language where the 3rd to last bit is a 1, which can be drawn as given below -

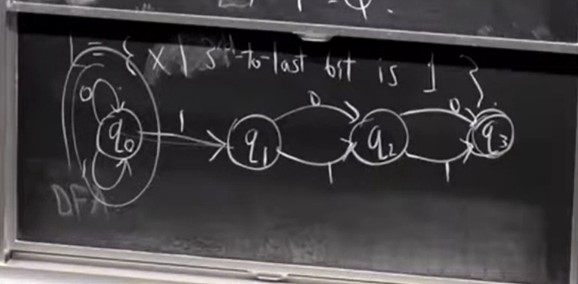
It turns out that NDFAs are essentially equivalent to DFAs. For every NDFA that accepts a language $L$, we can construct a DFA that accepts the same language, and for every DFA that accepts a language $L$, we can construct an NDFA that accepts the same language.

We do this by power set construction. First of all, converting from a DFA to an NDFA is trivial. All DFAs are NDFAs. To convert from an NDFA to a DFA, we construct a power set of the states the NDFA can be in. For example, if the NDFA can be in states {0, 1, 2}, then we construct a power set {0, 1, 2, 01, 02, 12, 012} (we exclude the null element in the power set). We can then convert from an NDFA to a DFA by following transitions from the start state of the NDFA, and whenever we read a character that can transition to multiple states, we jump to that element in the power set that has all of those states.

For example, if we consider the same NDFA given above, and we start at the start state and read a 1, we can end up in either the start state itself (state 0) or state 1. So in the DFA we transition to state 01.

An example conversion is shown below for the NDFA that accepts languages where the second to last bit is a 1 to its corresponding DFA.